
Inside the absolute value sign at x equals zero. The absolute value sign, just as if you didn't shift it, you would have had zero And at x equals negative three, you have zero inside This upward sloping line right over here. Gonna get a positive value and so that's why you have Now for x is greater than negative three, when you add three to it, you're That's why you have thisĭownward line right over here. Take it's opposite value and so that makes sense. Below x equals negative three, for x values less than negative three, what we're gonna have here, is this inside of the absolute value sign, is going to be negative and so then we're gonna Value sign is negative, we're gonna have a slope ofĮssentially negative one. Value sign is positive, we're going to getĮssentially, this slope of one. When whatever we have inside the absolute So if we shift three to the left, it's gonna look something like.

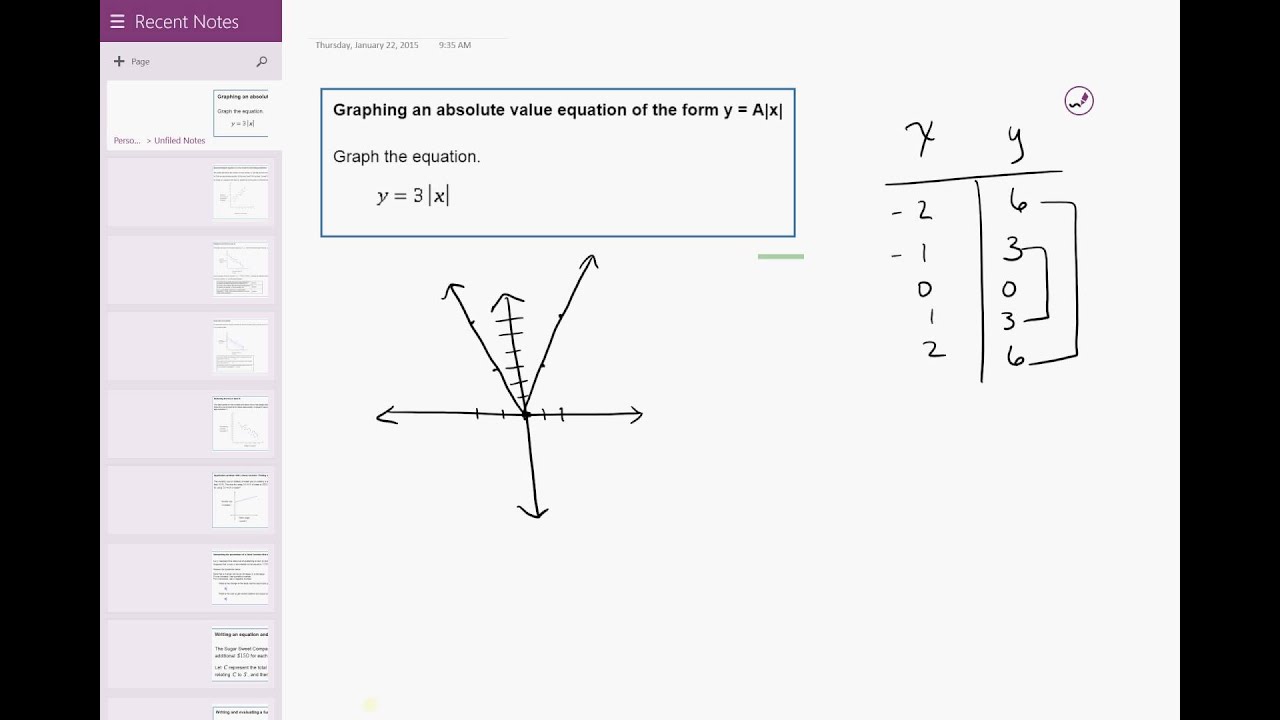
And we're gonna do that right now and then we're gonna just gonnaĬonfirm that it matches up. Subtracting from this x, that is how much you are shifting it. You could view this as the same thing as y is equal to the absolute

If you replace your x, with an x plus three, this is going to shift your So the next thing I wanna graph, let's see if we can graph y. And what they've already graphed for us, this right over here, this is the graph of y is equal To graph f of x is equal to two times the absolute value To actually put numbers onto this, you would lookk at your equation to get the vertex of the function (6, -10) and use the positive and negative slope to draw the two parts of the function. So our correct graph should be less steep than a normal absolute value function, and translated down and to the right. Since we have a low (<1) coefficient inside the function, the graph will horizontally get squished, or vertically stretch. While a high coefficient on the outside would increase every y-value by a certain factor (vertically stretch the graph), a high coefficient on the inside would increase every x-value by a certtain factor (horizontally stretch, which makes the graph wider). Now that the equation has been simplified to y = |1/2 (x - 6)| - 10, you can get to graphing.įor any function, if you have a coefficient inside the operation of the function (the absolute value bars in this case), it basically does the opposite of a coefficient on the outside. Because absolute value doesn't care about the sign, you can effectively just remove the negative on the 1/2. Now you're taking the absolute value of something (x - 6) times a negative. If you do that to this problem, you'll get this:
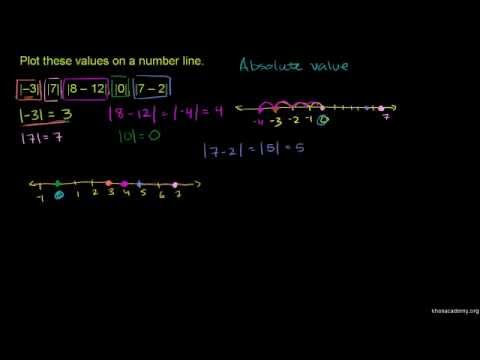
If you have a coefficient of x inside the absolute value sign, one thing you can do is try and isolate it a little bit, by setting it as a factor to the rest of the inside of the absolute value. I'll assume you're asking how to graph the equation.


 0 kommentar(er)
0 kommentar(er)
